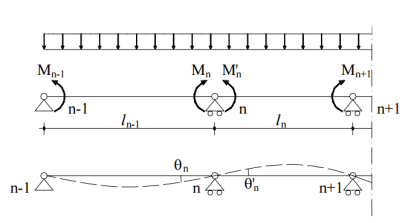
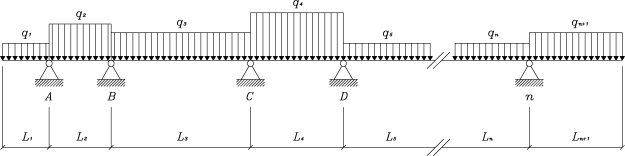
Nell’ambito della dinamica delle strutture, è inevitabile parlare di modi di vibrare, frequenze e periodi: tuttavia, quando si affrontano problemi e strutture semplici, come una trave, sia essa a mensola, semplicemente appoggiata o doppiamente incastrata, l’analisi FEM può portare facilmente a risultati poco realistici. In realtà è più corretto, anziché parlare di strutture semplici, di strutture ove complessivamente non è lecito fare l’assunzione/ipotesi che la maggior parte della massa sia concentrata a determinati livelli come gli impalcati di un edificio: in una trave doppiamente incastrata infatti possiamo invece dire che la massa da eccitare è distribuita lungo lo sviluppo della trave, e si può ricercare in questo caso particolare (come altri semplici) uno sviluppo analitico degli infiniti modi di vibrare e associate forme modali, ma se apriamo SAP2000 e disegnamo una trave, e lanciamo l’analisi… non succede nulla! Non calcola nemmeno il Load Case – MODAL. Ma perché?
La risposta è intrinseca nella formulazione del FEM: ragionando per funzioni di forma, i risultati dell’analisi dipendono dagli spostamenti dei nodi degli elementi frame sotto le varie situazioni. Tuttavia, se abbiamo un solo elemento frame incastrato ai due estremi, questi sono fissi e pertanto non viene nemmeno effettuato il calcolo. Ovviamente non è che SAP2000 non riesce a calcolare una trave doppiamente incastrata e sviscerarne gli aspetti, ma bisogna come sempre sapere cosa si fa: la prima cosa che potrebbe venire a mente sarebbe quella di dividere la trave incastrata in due, ed effettivamente adesso il calcolo parte, visto che adesso vi è il nodo di mezzeria non esternamente vincolato. Però… per quanti modi di vibrare avessimo tentato di trovare, ne troviamo solo tre. Questo cozza con la banalità del fatto che una trave, essendo un sistema continuo, possiede infiniti modi di vibrare, e noi ne troviamo solo 3. Quindi, evidentemente, c’è qualcosa che non va: ma ancora una volta non è il programma a sbagliare, ma noi che, introducendo pochissimi nodi esternamente svincolati, possono essere effettivamente calcolati solo 3 modi di vibrare. Inoltre, se confrontiamo la soluzione analitica in termini di periodo con quella trovata dal SAP… beh, è sballata!
A tal proposito, occorre effettivamente fare una modellazione più accurata: all’aumentare della suddivisione interna della trave, infatti, possiamo giungere a risultati sempre più vicini a quelli analitici, e trovare effettivamente un elevato numero di modi di vibrare: eppure la struttura è sempre la stessa, una trave doppiamente incastrata! Suddividerla in un numero sempre maggiore di elementi equivale grossomodo come operazione a “distribuire” la massa sull’elemento stesso, spalmarla, e pertanto ottenere dei risultati dal modello sempre più rappresentativi del reale comportamento della struttura. Ovviamente, lo stesso approccio non avrebbe molto senso in un edificio classico con impalcati in calcestruzzo, infinitamente rigidi nel loro piano: suddividere in molti elementi i pilastri, o ancor più le travi, non porta assolutamente agli stessi benefici in termini di rappresentatività, e pertanto possiamo lasciare i pilastri e le travi come elementi frame singoli riuscendo comunque ad avere un’approssimazione accettabile dei risultati.
Successivamente, potremmo provare a fare una modellazione con elementi brick, più per curiosità che per effettiva utilità: infatti la trave è in genere ben approssimabile ad un elemento monodimensionale, e lo sforzo maggiore di calcolo non trova una ragione (ovvero approssimazioni migliori) nella pratica. Tuttavia, possono occorrere anche qua dei problemi: infatti risulta molto importante la distribuzione spaziale degli elementi. Una distribuzione, ad esempio in sezione, degli elementi con una rigidezza prevalente in una dimensione rispetto all’altra, può portare a risultati anche qua sballati. Risulta perciò migliore una distribuzione senza direzioni privilegiate, al fine di cogliere meglio il comportamento. Un problema simile può avvenire ad esempio con una sezione quadrata e l’utilizzo degli operatori di meshatura DALL e SURF in CAST3M*: se non vi è un controllo su tale meshatura, DALL può creare dei problemi, senza che vi sia possibilità di accorgersene (a meno ovviamente del controllo umano).
Per approfondire, potete sfogliare l’ottimo libro di Rugarli, Analisi modale ragionata, che fa esempi diversi e argomentati direttamente con i numeri anche in caso di elementi shell. Le formule risolutive per una trave doppiamente incastrata e gli altri casi di carico sono mostrate nell’immagine qua sotto, dove 
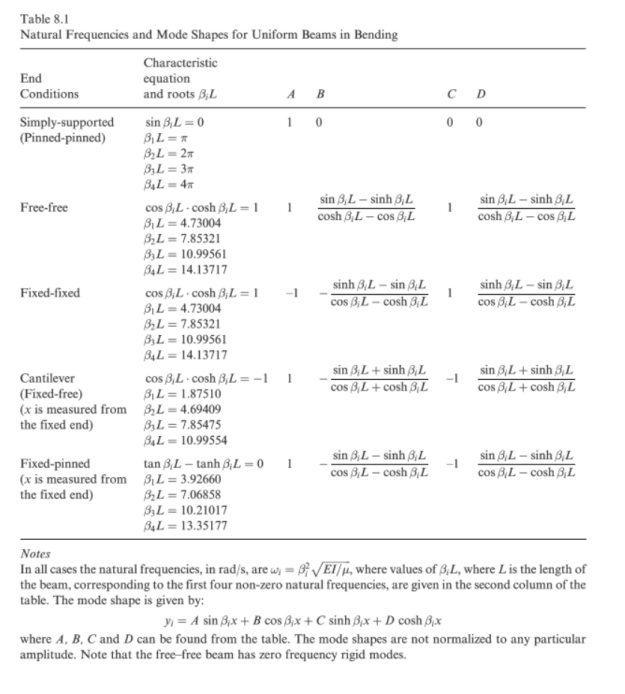
Immagine tratta da Structural Dynamics and Vibration in Practice: An Engineering Handbook – D. Thorby – 2008
Questo piccolo esempio/chiacchierata/mini-riflessione serve a ribadire ancora una volta, specie per chi ha pochissima dimestichezza col FEM, che una buona modellazione è fondamentale per ottenere risultati accettabili, ma che buona modellazione non significa riproduzione della geometria effettiva: ed è per questo motivo che credo che i software BIM non troveranno mai un’applicazione diretta in ambito strutturale, poiché anche la modellazione più banale comporta delle scelte che variano in base alla struttura, e devono essere governate da chi effettivamente sta creando il modello. Il BIM pertanto, con tutte le sue pretese di automatismo, se avesse a disposizione dei supercomputer per ogni cosa potrebbe forse trovare un reale approccio strutturale, ma fino ad allora penso che sia uno strumento utilissimo per pianificare, controllare e governare la progettazione architettonica ed impiantistica, e contemporaneamente aiutare la progettazione strutturale solo in termini di riduzione degli errori fra i vari passaggi negli elaborati, consentendo un flusso progettuale più regolare, ma ancora lontano dall’integrazione strutturale diretta.
*: CAST3M è un programma agli elementi finiti estremamente avanzato che funziona esclusivamente per riga di comando, più o meno come Code_Aster, ma con un linguaggio proprietario.
è (una delle possibili scritture):
appoggi con lettere progressive, mentre i vari tratti della trave continua con numeri progressivi. Questo per mettere in risalto la numerazione differente degli appoggi da quella dei carichi e delle lunghezze; chiaramente, per fare qualche esempio, 
. È importante affinché quanto di seguito abbia significato generale che la numerazione non cambi, in quanto alla fine quando propongo la formulazione generale in 
si deve aver capito tale sistema.
, ottenendo così un risultato corretto e contemporaneamente non far “scorrere” la numerazione impostata):
| Engineering | and | Architecture | 