Archivi tag: Equazione

L’equazione dei 3 momenti in Excel

9 Repliche

In questo articolo esporrò una variazione alla “classica” forma della nota equazione dei 3 momenti formulata da Clapeyron, che, come sappiamo, in una trave continua su più appoggi rigidi e con E, J = cost è (una delle possibili scritture):

\dfrac{1}{24}\Big( q_{n-1}L_{n-1}^{3} + q_{n}L_{n}^{3} \Big)=\dfrac{1}{6}\Big( L_{n-1}M_{n-1} + L_{n}M_{n+1} \Big)+\dfrac{1}{3}\Big( L_{n-1} + L_{n}\Big)M_{n}

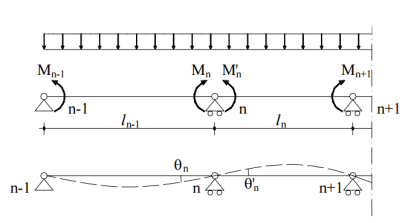
blabla

Non espongo la dimostrazione (che si basa sul principio di sovrapposizione degli effetti), in quanto esistono numerosissime risorse in rete che trattano l’argomento, pertanto reputo inutile riproporlo; al massimo, posso segnalarvi un’esposizione chiara qui.

Implementando però questa equazione su Excel con l’intenzione di creare un foglio “generale”, cioè che risulta valido per un numero generico di campate, mi sono trovato in difficoltà: infatti, scrivendo il foglio Excel, se non conosco a priori il numero delle campate, l’equazione implementata in questa forma non funziona, e risulta necessario creare un nuovo foglio per ogni casistica, in quanto conoscendo le condizioni al contorno (condizioni all’inizio e alla fine della travata e numero di campate) posso impostare il problema. Inoltre, volevo evitare di scrivere macro in Excel, in quanto avrebbe comportato il dover imparare VBA per Excel, cosa che ho intenzione di fare in futuro quando avrò più tempo, ma non ora.

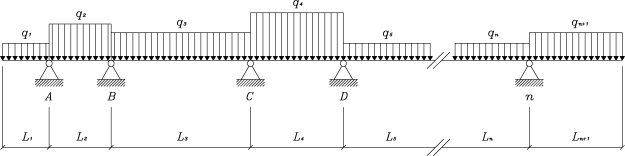
Ho tentato quindi di scrivere la sopracitata equazione in maniera “più digeribile” e più facilmente implementabile in un foglio di calcolo, che fosse indipendente dal numero di campate. Ho identificato gli n appoggi con lettere progressive, mentre i vari tratti della trave continua con numeri progressivi. Questo per mettere in risalto la numerazione differente degli appoggi da quella dei carichi e delle lunghezze; chiaramente, per fare qualche esempio, M_{A}=M_{1}, M_{B}=M_{2},etc. . È importante affinché quanto di seguito abbia significato generale che la numerazione non cambi, in quanto alla fine quando propongo la formulazione generale in i si deve aver capito tale sistema.

Si può notare intanto che sul primo appoggio A conosciamo sempre il valore del momento, che vi sia o meno uno sbalzo (infatti, se lo sbalzo è assente, basterà impostare che L_{1}=0, ottenendo così un risultato corretto e contemporaneamente non far “scorrere” la numerazione impostata):

M_{A} = \dfrac{q_{1}L_{1}^2}{2}

Successivamente, il secondo appoggio B, con opportuni e semplici passaggi matematici, possiamo arrivare a:

M_{B}=\dfrac{1}{L_{2}+L_{3}}\Bigg(\dfrac{q_{2}L_{2}^{3}}{8}+\dfrac{q_{3}L_{3}^{3}}{8}-\dfrac{M_{A}L_{2}}{2}-\dfrac{M_{C}L_{3}}{2}\Bigg)

Isoliamo quindi il termine relativo al momento in C:

M_{B}=\dfrac{1}{L_{2}+L_{3}}\Bigg(\dfrac{q_{2}L_{2}^{3}}{8}+\dfrac{q_{3}L_{3}^{3}}{8}-\dfrac{M_{A}L_{2}}{2}\Bigg)-\dfrac{L_{3}}{2 (L_{2}+L_{3})}M_{C}

e semplifichiamo il tutto introducendo il nuovo coefficiente

M_{B}^{*}=\dfrac{1}{L_{2}+L_{3}}\Bigg(\dfrac{q_{2}L_{2}^{3}}{8}+\dfrac{q_{3}L_{3}^{3}}{8}-\dfrac{M_{A}L_{2}}{2} \Bigg)

E quindi il momento in B è

M_{B}=M_{B}^{*}-\dfrac{L_{3}}{2 (L_{2}+L_{3})}M_{C}

Adesso possiamo ripetere passaggi simili per l’appoggio C, ottenendo:

M_{C}=\dfrac{1}{L_{3}+L_{4}}\Bigg(\dfrac{q_{3}L_{3}^{3}}{8}+\dfrac{q_{4}L_{4}^{3}}{8}-\dfrac{L_{3}}{2}\Bigg(M_{B}^{*}-\dfrac{L_{3}}{2 (L_{2}+L_{3})}M_{C}\Bigg)-\dfrac{L_{4}M_{D}}{2}\Bigg)=\dfrac{1}{L_{3}+L_{4}}\Bigg(\dfrac{q_{3}L_{3}^{3}}{8}+\dfrac{q_{4}L_{4}^{3}}{8}-\dfrac{L_{3}}{2}M_{B}^{*}-\dfrac{L_{4}M_{D}}{2}\Bigg)+\dfrac{1}{L_{3}+L_{4}}\cdot\dfrac{L_{3}^{2}}{4 (L_{2}+L_{3})}M_{C}

Introduciamo altri due coefficienti

\alpha_{0} = 1

\alpha_{1} = \dfrac{1}{\Big(1-\frac{L_{3}^{2} \cdot \alpha_{0}}{(L_{3}+L_{4}) \cdot 4 (L_{2} + L_{3})}\Big)}

Portando a sinistra tutti i termini per il momento in C e dividendo ambo i membri, si ottiene

M_{C} = \dfrac{\alpha_{1}}{L_{3} + L_{4}} \Bigg( \dfrac{q_{3}L_{3}^{3}}{8} + \dfrac{q_{4}L_{4}^{3}}{8} -\dfrac{L_{3}}{2} M_{B}^{*}\Bigg)-\dfrac{\alpha_{1}}{L_{3} + L_{4}}\dfrac{L_{4}M_{D}}{2}

Come sopra, creiamo un coefficiente fittizio per il momento in C

M_{C}^{*}=\alpha_{1}\cdot\dfrac{1}{L_{3}+L_{4}}\Bigg(\dfrac{q_{3}L_{3}^{3}}{8}+\dfrac{q_{4}L_{4}^{3}}{8}-\dfrac{L_{3}}{2} M_{B}^{*}\Bigg)

E quindi

M_{C} = M_{C}^{*}-\dfrac{\alpha_{1}}{L_{3}+L_{4}}\dfrac{L_{4}M_{D}}{2}

Procedendo per gli appoggi successivi a C, si nota una sorta di ricorsività nella formula, sempre semplificabile nella forma cui sopra; quindi possiamo scrivere, per gli i appoggi successivi a C

Per \begin{cases} i \geq 3 \\ i < n \end{cases}

M_{i} = \dfrac{\alpha_{i-2}}{L_{i} + L_{i+1}} \Bigg( \dfrac{q_{i}L_{i}^{3}}{8} + \dfrac{q_{i+1}L_{i+1}^{3}}{8} -\dfrac{L_{i}}{2} M_{i-1}^{*}\Bigg)-\dfrac{\alpha_{i-2}}{L_{i} + L_{i+1}}\dfrac{L_{i+1}M_{i+1}}{2}

M_{i}^{*}=\alpha_{i-2}\cdot\dfrac{1}{L_{i}+L_{i+1}}\Bigg(\dfrac{q_{i}L_{i}^{3}}{8}+\dfrac{q_{i+1}L_{i+1}^{3}}{8}-\dfrac{L_{i}}{2} M_{i-1}^{*}\Bigg)

\begin{cases} \alpha_{0}=1\\\alpha_{i-2}=\dfrac{1}{\Big(1-\frac{L_{i}^{2} \cdot \alpha_{i-3}}{(L_{i}+L_{i+1}) \cdot 4 (L_{i} + L_{i-1})}\Big)} \end{cases}

Questa struttura dell’equazione dei tre momenti è facilmente implementabile, in quanto è necessario solamente definire cosa succede nei primi due appoggi e l’ultimo affinché la travata sia risolta.

M_{A} = \dfrac{q_{1}L_{1}^2}{2}

M_{B}=M_{B}^{*}-\dfrac{L_{3}}{2 (L_{2}+L_{3})}M_{C}

M_{B}^{*}=\dfrac{1}{L_{2}+L_{3}}\Bigg(\dfrac{q_{2}L_{2}^{3}}{8}+\dfrac{q_{3}L_{3}^{3}}{8}-\dfrac{M_{A}L_{2}}{2} \Bigg)

M_{n} = \dfrac{q_{n+1}L_{n+1}}{2}

Il problema è così definito per tutti gli appoggi, a prescindere dal loro numero.

Come prevedibile poi, ho implementato quanto sopra in un foglio Excel:

Trave continua 1.00

Ovviamente questo cui sopra è solamente un esempio, e potete costruirvi un foglio Excel sulla sua falsariga ben più complesso, con grafici e quant’altro.

[1]: L’equazione di Clapeyron è valida anche in travi continue eterogenee ed a sezione variabile, ma ovviamente la formula è diversa. Nel PDF segnalato vi sono tutti i passaggi anche per questo caso.